Introduction
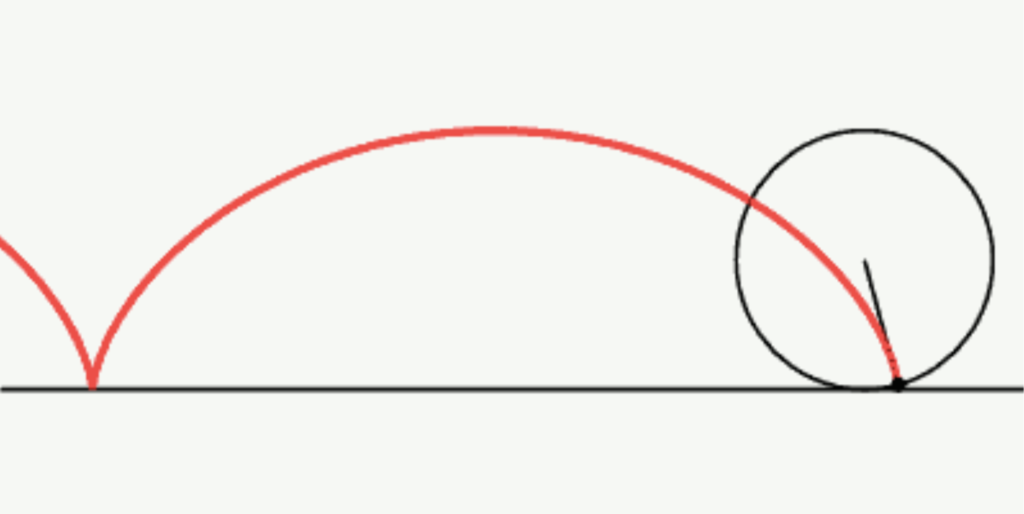
A cycloid is a shape (a curve) that is made by the path traced by a fixed point on the circumference of a circle that rolls (without slipping) on a flat surface.
One of the most famous pairs of problems of calculus share its involvement of a cycloid in their solutions.
The proof requires calculus out of the scope of high school math, so the emphasis of this article is on the explanation of the problem, its implications and the starting ideas that led to the solution.

The Brachistochrone Problem
The Brachistochrone problem was posed by mathematician Johann Bernoulli in 1696 as a challenge for other mathematicians at the time. The problem was to find the path that would require an object under the influence of gravity (only) the least amount of time to travel from one point to another. Brachistochrone means ‘shortest time’ in Ancient Greek.
Galileo once predicted that the arc of a circle would be optimal, but this turned out to be incorrect. The problem was solved correctly by Newton, L’Hopital, Leibniz, James Bernoulli, and Johann himself.
The solution relied on a principle that Fermat established in 1662. The principle stated that a beam of light would choose to follow the path that would take the least time when travelling from one point to another. Snell’s law, following Fermat’s, explained the path of light when it was refracted: the fastest possible path would be when sin(θ)/v is kept constant (where θ is the angle between the light ray and the vertical, and v is the speed of light in that particular medium).
Here, the velocity of an object at some point is proportional to the square root of the vertical distance from the starting point (by equating kinetic energy [(½)mv^2] and gravitational potential energy [mgy]). This means that if sin(θ)/v must be constant, sin(θ)/sqrt(y) must also be constant. Johann Bernoulli realised that this was similar to the differential equation of a cycloid.
The Tautochrone Problem
The Tautochrone problem was to find a curve where the time it takes for an object to slide down in uniform gravity (and without friction) to the lowest point is the same wherever they start off on the curve. One of the motivations of this problem was to find an isochronous pendulum, which means that the period of oscillation stays constant regardless of its amplitude (the highest point the pendulum reaches in oscillation). This condition was similar to simple harmonic motion, which was how the solution was explored.
This problem was solved by Christian Huygens in 1659, and this problem was solved before the Brachistochrone problem. Friction and other factors made it difficult to test in real life, so this problem was solved analytically. The solution curve turned out to be a cycloid. The time it takes to reach the bottom is π*sqrt(r/g), where r is the radius of the circle (creating the cycloid) and g is the gravitational acceleration, and this is the same amount of time a pendulum with simple harmonic motion would take to travel the same path.
[1] 3Blue1Brown. (2016). “The Brachistochrone, with Steven Strogatz”. https://www.youtube.com/watch?v=Cld0p3a43fU. Last Accessed: 2020/04/17.
[2] “Tautochrone Problem”. Wolfram Mathworld. https://mathworld.wolfram.com/TautochroneProblem.html. Last Accessed: 2020/04/17.
[3] “Brachistochrone Problem”. Wolfram Mathworld. https://mathworld.wolfram.com/BrachistochroneProblem.html. Last Accessed: 2020/04/17.
[4] “Cycloid”. Wolfram Mathworld. https://mathworld.wolfram.com/Cycloid.html. Last Accessed: 2020/04/17.
[5] [IMAGE] “A cycloid generated by a rolling circle”. https://en.wikipedia.org/wiki/Cycloid#/media/File:Cycloid_f.gif.