Fermat's Last Theorem
Fermat’s Last Theorem was originally created by French mathematician Pierre de Fermat in 1637 which states that in the following equation [a^n + b^n = c^n], no three positive integers a, b, and c can satisfy this equation given that n is any integer greater than 2.
Fermat discovered this as he was taking a glance at the Pythagoras theorem and also came up with a proof for it. In his book, Arithmetica however, it only states that “I know how to prove this marvelous equation, except I don’t have enough space to write the proof”. Fermat however, passed away before he could show anyone this proof and mathematicians weren’t able to prove this theory for over 300 years. After Fermat’s death, his son published a new version of Arithmetica, which included all the notes Fermat had made in his career, and mathematicians were indeed able to figure out the missing proofs for his theorems (Fermat initially had a lot of other “unproven” theories). This however, was not the case for Fermat’s Last Theorem. Fermat’s Last Theorem got its name from the fact that it was the last of Fermat’s theorems to be proved. Fermat’s last theorem became the most famous math problem among mathematicians, until an Oxford mathematician Andrew Wiles established a proof for it in 1995. In order to solve this complex theorem, Wiles first had a look at the Taniyama-Shimura conjecture, which is now known as the modularity theorem for elliptic curves.

In order to grasp some understanding of the modularity theorem, consider a sinusoidal function in an infinite plane (see fig. 1). If one were to break up the infinite plane into equal pieces of rectangles, the wave function will look the same for any pieces of plane we cut out. We call this kind of situation a translational symmetry.
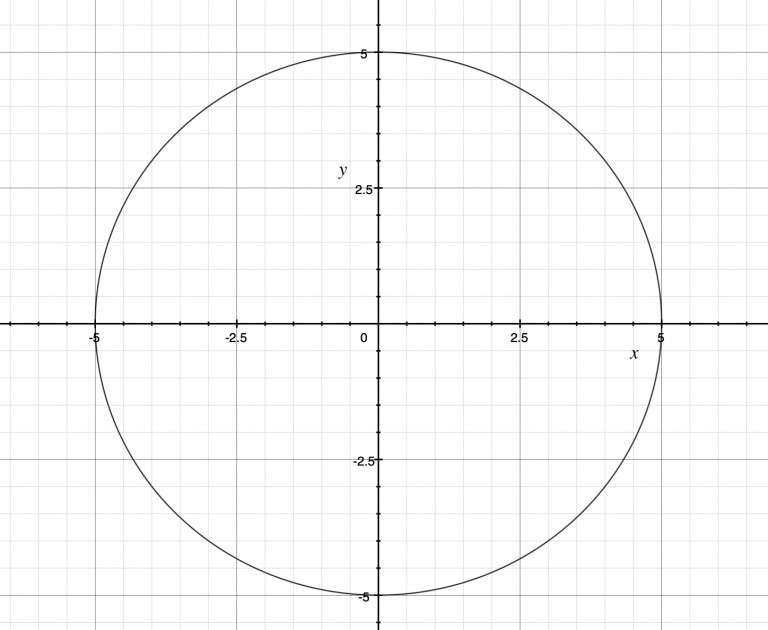
Now, consider a circle (see fig.2). Different from the sinusoidal function, if we were to cut the infinite plane into equal sizes of smaller planes, each plane will not look identical. Imagine if you were to take some point on the edge of the circle and allow it to rotate along the circumference at constant speed. No matter how many times you let the point travel along the circumference of the circle, the shape of this figure stays a circle. However, if we were to take this to a 3-dimensional point of view and allow the point to move at a constant rate and slowly allow it to climb out of your screen, what you get is a slinky-like shape (let’s just call it a slinky for the sake of simplicity). If we were to look at the slinky from your right or left, the shape resembles a sine wave with translational symmetry. However, if you were to look straight inside the slinky, you can see that the slinky stays as a circle. By using this method, you can essentially view a 3D object as if it were in 2D, and therefore as a result, you can fit a function that has translational symmetry into some other function that does not have translational symmetry.
This method of fitting an equation into another equation that has no resemblance was vital for Willes to prove Fermat’s Last Theorem.
The Catalan Conjecture
Catalan’s theorem was established by a French and Belgian mathematician Eugene Charles Catalan in 1844 and was not proven by 2002. The theorem says that in the following equation [x^a – y^b = 1], x = 3, a = 2, y = 2, b = 3 are the only set of solutions for a, b > 1 and x, y > 0.
The way to approach the problem is to first consider an equation [x^2 – y^3 = 1] and write the equation as a function of y, and then factorize x^2 – 1 = y^3 to (x – 1)(x + 1)=y^3. If we assume that y is an odd number, both (x-1) and (x+1) must be a number that was obtained by taking some number to its 3rd power. In addition, the difference between the two numbers must be 2. If we take a look at the sequence of numbers listed on your right however, ( [1^3 = 1, 2^3 = 8, 3^3 = 27, 4^3 = 64….] ) there are no such pairs of numbers with a difference of 2. It is also worth noting as the numbers increase, the difference between the two numbers with a power of 3 increases as well. We can therefore, eliminate the fact that y is an odd number. All in all, the important technique that is used in the actual proof is to put y in one side and the other terms to the other side to rewrite the equation.
Moving Sofa Problem
Imagine you have to fit a large sofa to make a 90 degree turn at your hallway. For small sofas, this wouldn’t be a problem. But this turn may be impossible if the sofa is too large. Given the width of the hallway to be 1, what is the largest two-dimensional area of the sofa you could fit and make a turn in the corner (the sofa can be in any shape)?
The answer to this problem is represented in something that is called the sofa constant (yes, it’s actually called the sofa constant). It is not known what the exact number of the sofa constant is, but we know that it is between 2.2195 and 2.8284.
Works Cited
[1] Thompson, Avery. (2016). “5 Simple Math Problems That No One Can Solve”. Popular Mechanics. https://www.popularmechanics.com/science/g2816/5-simple-math-problems/ Last Accessed: 14 Feb. 2020
[2] Numberphile. (2018). “The Heart of Fermat’s Last Theorem – Numberphile”. https://www.youtube.com/watch?v=ua1K3Eo2PQc&t=220s Last Accessed: 14 Feb. 2020
[3] Numberphile. (2018). “Catalan’s Conjecture – Numberphile”. https://www.youtube.com/watch?v=Us-__MukH9I&t=50s Last Accessed: 14 Feb. 2020
[4] Rocchini. (2007). “File: Hammersley sofa animated.gif”. Wikimedia Commons. https://commons.wikimedia.org/wiki/File:Hammersley_sofa_animated.gif Last Accessed: 14 Feb. 2020.
Thumbnail Image Source
[5] Elchinator. “Math Work Mathematics Formula – Free photo on Pixabay”. Pixabay. https://pixabay.com/photos/math-work-mathematics-formulas-4711302/ Last Accessed: 6 Aug. 2020.
